Olimpiade Matematika Tingkat SD dan SMP se Kabupaten Bima

Dalam rangka pengembangan mutu sumber daya manusia Indonesia sehingga mampu bersaing dalam era keterbukaan dan globalisasi dewasa ini, sangat diperlukan adanya terobosan-terobosan kreatif dari berbagai lembaga pendidikan. Pemerintah telah memfasilitasi lembaga-lembaga pendidikan agar terus melakukan berbagai terobosan yang menjamin adanya peningkatan mutu pendidikan melalui Undang-Undang nomor 20 tahun 2005 dan berbagai peraturan turunannya. Dengan adanya jaminan peningkatan mutu pendidikan yang diselenggarakan oleh berbagai lembaga pendidikan yang ada di Indonesia, maka harapan tercapainya manusia Indonesia yang berdaya saing pada percaturan regional dan internasional akan mampu tercapai.

Musyawarah Guru Mata Pelajaran (MGMP) Matematika SMP se Kabupaten Bima Wilayah barat yang mewadahi guru-guru matematika SMP yang ada di wilayah Kecamatan Bolo, Mada Pangga, Donggo, Soromandi, Sanggar dan Tambora berupaya untuk ikut serta menjamin terwujudnya manusia Indonesia yang berdaya saing regional dan internasional sebagaimana yang diamanatkan oleh Undang-Undang Nomor 20 Tahun 2005 beserta sejumlah peraturan turunannya. Salah bentuk upaya tersebut adalah menjamin bahwa mutu pembelajaran yang dikelola oleh para guru matematika SMP yang tergabung dalam MGMP Matematika Bima Barat adalah pembelajaran mampu menghasilkan siswa yang mampu berdaya saing secara regional dan internasional.

Sebagai salah satu wujud penjaminan mutu pembelajaran yang dikelola oleh anggota MGMP Matematika SMP Bima Barat adalah dengan adanya penyelenggaraan perlombaan Olimpiade Matematika Tingkat SD dan SMP se Kabupaten Bima. Perlombaan tersebut bertujuan untuk mencari bibit-bibit unggul dalam bidang matematika yang akan dipersiapkan dalam perlombaan Olimpiade Sains Nasional (OSN) yang secara reguler diselenggarakan oleh pemerintah setiap tahunnya. Di samping itu, kegiatan tersebut juga diharapkan menjadi alat evaluasi bagi para guru berkaitan dengan mutu pembelajaran yang telah dikelolanya.

Melalui kegiatan perlombaan tersebut diharapkan nantinya ada perwakilan Kabupaten Bima yang mampu meraih medali bidang matematika dalam ajang perlombaan OSN tingkat nasional. Prestasi seperti itu selama ini masih menjadi mimpi bagi Kabupaten Bima, karena belum pernah terjadi selama penyelenggaraan OSN ada siswa dari Kabupaten Bima yang berhasil meraih prestasi tersebut. Prestasi sebagai pemegang medali OSN bidang matematika ibarat tembok besar yang masih sulit diruntuhkan oleh siswa asal Kabupaten Bima.

Salah satu kendala terbesar yang dialami oleh para guru dalam pembinaan siswa peserta OSN bidang Matematika selama ini adalah kurangnya sarana uji coba. Sehingga adanya perlombaan Olmipiade Matematika Tingkat SD dan SMP se Kabupaten Bima yang diselenggarakan oleh MGMP Matematika Bima Barat bisa menjadi alat uji coba bagi calon peserta OSN bidang Matematika asal Kabupaten Bima. Kendala terbesar dari tidak adanya kegiatan serupa itu di Kabupaten Bima adalah kurangnya sponsor yang mau memberikan dukungan pada kegiatan tersebut. Tanpa adanya sponsor yang mendukung, akan sangat sulit untuk diselenggarakan perlombaan dengan hadiah yang mampu memotivasi siswa untuk terus belajar dan berlatih.

Masalah hadiah itulah yang umumnya menjadi kendala dalam penyelenggaraan perlombaan semacam Olimpiade Matematika Tingkat SD dan SMP yang digagas oleh MGMP Matematika Bima Barat. Sebagai langkah memotivasi siswa calon peserta lomba sehingga mereka mau mempersiapkan diri dengan matang dan berjuang dengan gigih untuk menjadi terbaik, maka besar hadiah yang mereka terima ketika berhasil menjadi yang terbaik haruslah disebutkan terlebih dahulu. Salah satu penyebab rendahnya motivasi siswa dalam berlomba selama ini adalah karena ketika mereka berhasil menjadi yang terbaik, mereka hanya diberikan piagam dan piala saja.

Melalui kegiatan perlombaan anugrah pewarta Astra ini, saya selaku ketua MGMP Matematika SMP Bima Barat mengusulkan agar Astra bersedia menjadi sponsor utama penyelenggaraan Olimpiade Matematika Tingkat SD dan SMP se Kabupaten Bima yang digagas oleh MGMP Matematika Bima Barat. Harapan kami, Astra bisa memberikan hadiah uang tunai kepada para juara, yaitu juara 1 hingga juara 6 untuk tingkat SMP serta juara 1 hingga juara 6 untuk tingkat SD. Sebagai kompensasinya, kami akan mencantumkan dalam pengumuman lomba, lembar soal, pernak-pernik lomba bahwa perlombaan tersebut disponsori oleh Astra. Kami juga bisa menyediakan waktu kepada Astra untuk mempromosikan produknya kepada para guru matematika se Kabupaten Bima.

Buku Soal Kompetisi Matematika yang Wajib Anda Miliki

Saya ingin menawarkan sebuah buku soal kompetisi matematika yang sangat menarik dan berbobot. Buku ini berisi soal-soal kompetisi matematika tingkat internasional yang sangat populer, yaitu soal-soal elementary mathematics international contest (EMIC) mulai awal penyelenggaraan hingga tahun 2015, soal-soal Invitational world youth mathematics international contest (IWYMIC) juga mulai awal penyelenggaraan hingga tahun 2015, serta soal-soal po leung kuk primary mathematics world contest (PLK PMWC) mulai awal penyelenggaraan hingga tahun 2015.

Harga : 150.000

Jika anda berminat dapat menghubungi saya melalui nomor : 082340200444

Berikut sampel beberapa bagian buku

Pembahasan Soal OSN Matematika SMP Tingkat Propinsi Tahun 2014, Nomor 13

SOAL

Diberikan kerangka limas ABCD dengan alasnya adalah daerah segitiga siku-siku ABC. Diketahui sisi siku-sikunya adalah AB dan AC  dengan panjang AB = a√3 dan panjang AC = 4a, rusuk BD tegak lurus dengan bidang ABC, dan panjang BD = 6a. Jika pada rusuk CD terdapat titik P sehingga sebuah bola dengan DP sebagai diameternya menyinggung bidang alas ABC, hitung jari-jari bola tersebut.

PEMBAHASAN : LIHAT DI SINI

MOHON DIKOREKSI BILA SALAH

Pembahasan Soal OSN Matematika SMP Tingkat Propinsi Tahun 2014, Nomor 15

Soal :

Pembahasan : LIHAT DI SINI

SOAL PEMBINAAN OLIMPIADE MATEMATIKA (2)

1. Di dalam persegi dengan sisi 14cm terdapat setengah lingkaran dan dua seperempat lingkaran seperti tampak pada gambar di samping. Tentukan perbandingan luas daerah yang tidak diarsir dengan luas daerah yang diarsir !

2. Jika jarak antar titik-titik adalah 1cm, tentukan luas daerah pada gambar berikut !

3. ABCD.EFGH pada gambar disamping adalah sebuah balok. Jika luas ABCD = 33cm², luas ABFE = 24cm², dan luas BCGF = 22cm².

SOAL PEMBINAAN OLIMPIADE MATEMATIKA

1. Jelaskan proses perhitungan dan hasil dari

2. Umur Pino 3 tahun lebih tua dari umur Nanosamo, sedangkan umur Nanosamo 4 tahun lebih tua dari umur Pina. Tentukan umur Pino ketika Pina berumur 23 tahun.

3. Sancai menjual hasil kebunnya setiap tiga hari sekali dan Sato menjual hasil kebunnya setiap empat hari sekali. Pada hari Minggu mereka bertemu pertama kalinya di pasar. Pada hari apa mereka bertemu kembali di pasar tersebut untuk ketiga kalinya ?

Pembinaan Olimpiade Matematika : Teori Bilangan

1. UJI HABIS DIBAGI

a. Suatu bilangan habis dibagi 5 jika dan hanya jika digit terakhir dari bilangan tersebut adalah 0 atau 5

Contoh : 67585 dan 457830 adalah bilangan-bilangan yang habis dibagi 5.

b. Suatu bilangan habis dibagi 2ⁿ jika dan hanya jika n digit terakhir dari bilangan tersebut habis dibagi 2ⁿ.

Contoh : 134576 habis dibagi 8 = 2³ sebab 576 habis dibagi 8 (576 : 8 = 72)

4971328 habis dibagi 16 = 2⁴ sebab 1328 habis dibagi 16

c. Suatu bilangan habis dibagi 3 jika dan hanya jika jumlah digit bilangan tersebut habis dibagi 3.

Contoh : 356535 habis dibagi 3 sebab 3 + 5 + 6 + 5 + 3 + 5 = 27 dan 27 habis dibagi 3.

d. Suatu bilangan habis dibagi 9 jika dan hanya jika jumlah digit bilangan tersebut habis dibagi 9.

Contoh : 23652 habis dibagi 9 sebab 2 + 3 + 6 + 5 + 2 = 18 dan 18 habis dibagi 9.

e. Suatu bilangan habis dibagi 11 jika dan hanya jika selisih antara jumlah digit dari bilangan tersebut pada posisi ganjil dengan jumlah digit dari bilangan tersebut pada posisi genap habis dibagi 11.

Contoh : 945351 habis dibagi 11 sebab (9 + 5 + 5) − (4 + 3 + 1) = 11 dan 11 habis dibagi 11. Contoh bilangan lain yang habis dibagi 11 adalah 53713 dan 245784.

Soal Kompetisi Matematika

Soal-soal berikut adalah sebagian soal dari soal seleksi peserta OSN Jawa Barat tahun 2008. Sebagai sarana latihan, soal-soal berikut sangat bagus untuk membiasakan diri menghadapi berbagai model soal dalam lomba/kompetisi matematika. Selamat Mencoba.

 

Soal Isian Singkat

SOAL OLIMPIADE MATEMATIKA : PERSAMAAN ALJABAR

Jika a dan b bilangan bulat positif, tentukan semua pasangan (a , b) yang memenuhi persamaan berikut :

a – b = 1

2a² + ab – 3b² = 22

Seri Soal Olimpiade Matematika

SOAL 1

Hasil kali digit-digit dari 166 adalah 1 x 6 x 6 = 36.

Tentukanlah semua bilangan yang mungkin, antara 100 dan 1000, yang hasil kali digit-digitnya 36

 

SOAL 2

Delapan buah persegi A, B, C, D, E, F, G, dan H memiliki ukuran yang sama diletakan bertumpuk, sehingga ada yang saling tumpang tindih.

Berikut adalah penampakan tumpukan tersebut dari atas.

Urutan letak persegi-persegi tersebut dari atas ke bawah adalah …

 

Soal Olimpiade Matematika tentang Luas Segitiga dan Persegi Panjang

Soal berikut adalah soal tentang luas daerah persegi panjang dan segitiga. Soal berikut menjadi sangat menarik, karena dengan hanya menggunakan dua konsep yang sangat sederhana yaitu konsep luas persegi panjang dan segitiga, tetapi memerlukan penalaran yang sangat tinggi dalam penyelesaianya. Hampir semua siswa SD(kelas 5/6)/SMP telah hafal rumus luas persegi panjang dan segitiga, tetapi masih sangat kurang dalam ketrampilan menggunakan rumus-rumus tersebut dalam menyelesaikan soal.

Cobalah kerjakan soal berikut sebagai sebuah tantangan yang harus ditaklukan oleh siswa SD/SMP, bahkan siswa SMA pun bisa jadi akan kesulitan. Selamat mencoba.

SOAL

E, F, G, dan H adalah titik tengah masing-masing sisi persegi panjang ABCD. Dan K adalah titik tengah garis HE.

Jika persegi panjang ABCD memiliki luas 12 m², berapakah luas segitiga KFG?

 

Jawabannya adalah …

Soal Olimpiade Matematika Tentang Lingkaran

Dua soal berikut sangat bagus untuk mengasah pengetahuan tentang lingkaran. Cobalah dikerjakan!

SOAL – 1

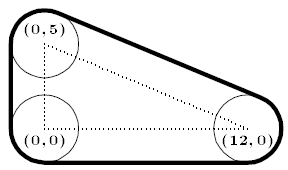
Pusat dari tiga buah lingkaran yang berjari-jari 2 terletak pada titik (0,0), (12,0), dan (0,5). Jika ketiga lingkaran tersebut adalah merupakan tiga buah kerekan, Berapa panjang sabuk yang digunakan untuk mengelilingi ketiga kerekan tersebut seperti yang ditunjukan pada gambar?

SOAL – 2

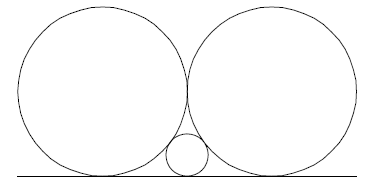
Dua buah lingkaran yang masing-masing berjari-jari 10 cm diletakan pada sebuah bidang datar dengan kedua lingkaran saling bersinggungan satu sama lain. Sebuah lingkaran kecil diletakan di antara kedua lingkaran besar tersebut sedemikian hingga lingkaran kecil menyinggung kedua lingkaran besar dan bidang datar. Berapakah jari-jari lingkaran kecil?

Jika ingin melihat jawaban dari kedua soal tersebut, silahkan klik kelanjutannya di bawah ini. Tapi jawaban tersebut belum pasti benar, untuk mari kita saling berbagi untuk memperkaya ilmu matematika kita